Desde el equilibrio de Nash hasta los límites de la propia teoría.
¿Alguna vez te has preguntado cómo tomar las mejores decisiones estratégicas en situaciones competitivas?
Pues la teoría de juegos responde precisamente a eso. Desde juegos de mesa hasta estrategias empresariales y políticas, esta teoría nos proporciona la herramienta perfecta para la toma de decisiones estratégicas.
En este artículo, exploraremos los conceptos fundamentales, aplicaciones prácticas y curiosidades de esta rama de las matemáticas. Aprenderemos todo sobre la teoría de juegos, incluido el famoso equilibrio de Nash
¡Prepárate para sumergirte en el apasionante mundo de la teoría de juegos!

¿Qué es la teoría de juegos y en qué consiste?
La teoría de juegos es una rama de las matemáticas que se encarga de analizar situaciones de toma de decisiones entre dos o más individuos. En muchas ocasiones, la teoría de juegos puede considerarse como la ciencia de la estrategia o, al menos, la ciencia que estudia la toma de decisiones eficientes.
La teoría de juegos se utiliza en multitud de casos en los que los que se requiere un pensamiento estratégico. En la rama económica, por ejemplo, es capaz de analizar la estabilidad (o inestabilidad) de un oligopolio o los efectos de las subastas.
Puede considerarse a John von Neumann como el padre de esta teoría. En 1944 publicó, junto al economista Oskar Morgenstern su artículo: “Teoría de Juegos y Comportamiento Económico”
La teoría continúo desarrollándose con el paso del tiempo, resultando fundamentales las aportaciones de John Nash, quien recibió el premio nobel gracias a sus aportaciones a esta teoría, acuñando por el camino el término de Equilibrio de Nash.
La forma matricial y la forma extensiva
La principal característica que define la teoría de juegos es que el resultado de las acciones individuales de cada jugador influye en el resultado del resto de jugadores.
Así, en un juego de dos jugadores, las acciones de A influirán en los resultados de B y las acciones de B en los de A. Normalmente, los juegos suelen presentarse utilizando matrices (representación matricial) o diagramas en forma de árbol (representación extensiva). La elección en la representación depende del tipo de juego, aunque eso es algo que posteriormente veremos con más detalle.
Forma Matricial
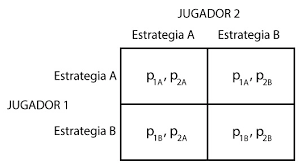
Juego representado en forma matricial.
En esta matriz puede verse un ejemplo de juego. Tenemos dos jugadores, el jugador 1 y el jugador 2, y cada uno puede elegir entre dos posibles estrategias, la A y la B. Como podemos ver, la matriz muestra todos los resultados posibles, en este caso cuatro.
Si tanto el jugador 1 como el jugador 2 escogiesen la estrategia A, recibirían respectivamente los pagos P1A y P2A. Como puedes ver, el objetivo de la matriz es mostrar cuales son los resultados que se obtendrían en cada uno de los posibles resultados.
Esta representación es la que se utiliza para los juegos simultáneos, que son aquellos en los que los dos jugadores realizan sus jugadas a la vez.
Forma Extensiva
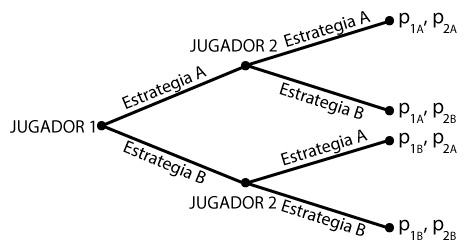
Juego representado en forma extensiva.
Ahora tenemos un diagrama en forma de árbol, donde cada nodo representa una situación en la que el jugador debe de tomar una decisión. En este caso, el jugador 1 tomaría primero su decisión y el jugador 2 la tomaría después de él. Podemos ver como los dos jugadores disponen de dos estrategias, la A y la B.
A la derecha del todo se muestran los pagos del juego, es decir, los resultados. Las dos imágenes que hemos visto muestran el mismo juego. La única diferencia es que en la primera imagen, el juego se plantea de forma simultanea y en la segunda , se muestra de manera secuencial (haciendo sus jugadas por turnos)
Aunque ahora te pueda parecer muy complejo, no te preocupes. Estas dos imágenes muestran juegos en su forma teórica, sin números ni resultados; lo que los hace un poco abstractos. Cuando veamos ejemplos con números reales te será mucho más fácil de comprender.
Antes de pasar a los ejemplos, es importante que veamos una serie de términos. La teoría de juegos es una disciplina académica propia y, como tal, tiene su propio lenguaje.
Términos Útiles en Teoría de Juegos
Estas son las palabras más utilizadas en la teoría de juegos. Con ellas ya podrás sonar como todo un experto al hablar de este tema.
Juego
Un juego es cualquier conjunto de circunstancias en la que los resultados dependen de las decisiones de dos o más jugadores. Por lo general, los juegos suelen clasificarse en base a sus características esenciales; como ya veremos más adelante.
Subjuego
Sabiendo lo que es un juego, no es difícil imaginar qué es un subjuego. Un subjuego es un juego que tiene lugar dentro de un juego.
Básicamente un subjuego es una parte de un juego que puede analizarse como un juego separado, para posteriormente incluir el resultado de este subjuego en el juego global y facilitar la toma de decisiones.
Ejemplo de juego dividido en subjuegos
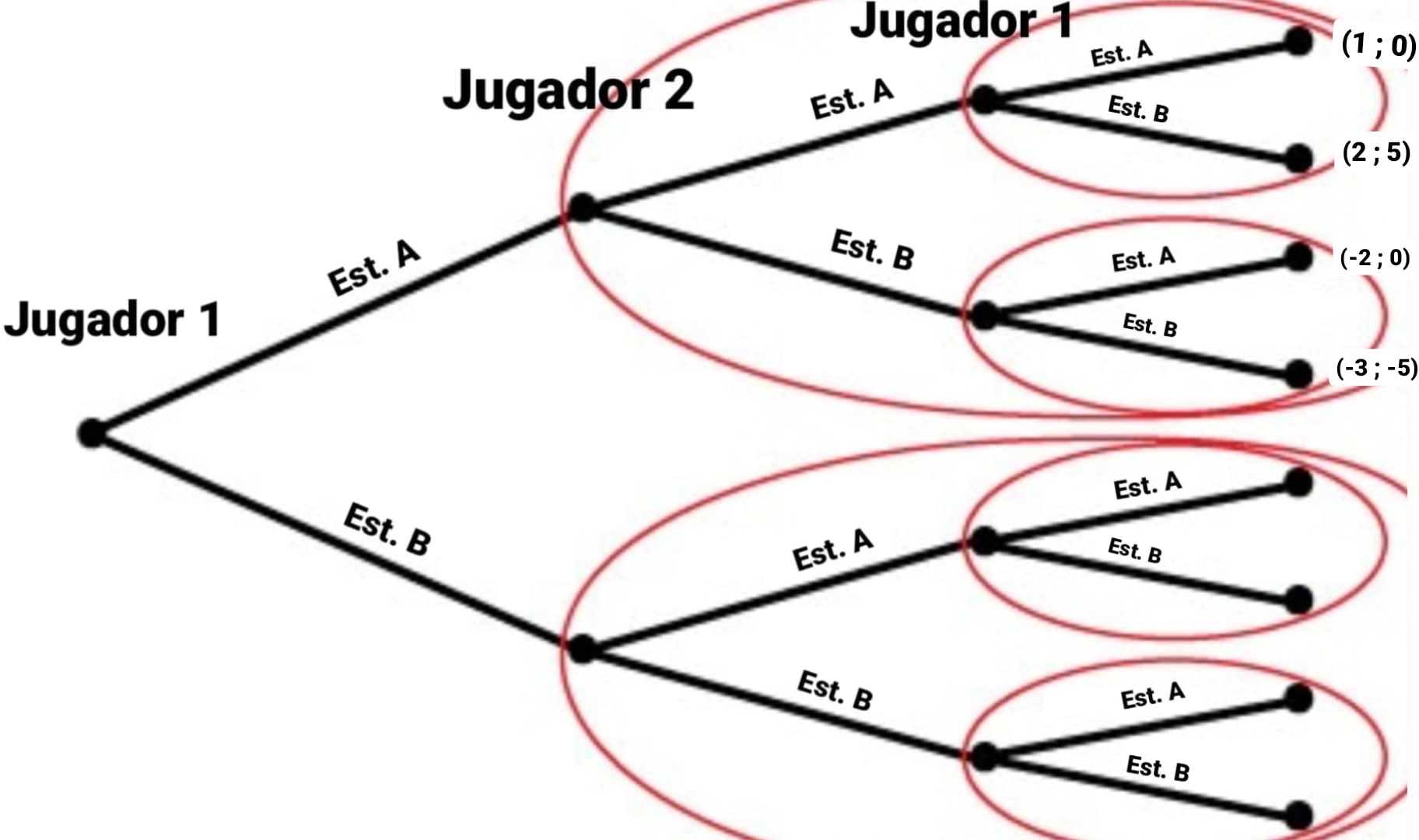
Juego dividido en subjuegos
En la imagen anterior podemos ver un juego secuencial entre dos jugadores, divido en subjuegos por cada círculo rojo. La división en subjuegos se realiza para poder resolver el juego paso a paso.
Resolución por subjuegos
Si nos vamos al primer subjuego del jugador 1, podemos ver que puede escoger entre 2 estrategias, A y B y que estas le reportarán un pago de 1 y 2 respectivamente.
La solución a este subjuego es muy sencilla, como es un individuo racional que busca maximizar sus ganancias, siempre escogerá la estrategia B.; por lo que la solución del subjuego sería la B (como veremos más adelante, esta “solución” es en realidad el equilibrio de Nash perfecto en este subjuego).
Lo mismo sucede para el juego de más abajo, en este caso debe elegir entre -2 y -3. Al buscar maximizar sus ganancias (que es equivalente a minimizar sus pérdidas) escogerá en este caso la estrategia A, con la que pierde menos.
Podemos así, simplificar el primer subjuego en el que participa el jugador 2. Ya sabemos las opciones que tomará el jugador 1 y también conocemos los pagos asociados al jugador 2.
En este caso, si el jugador 2 elige la estrategia A, el jugador 1 escogerá la estrategia B (como hemos demostrado antes) y su pago será de 5. En el caso de que el jugador 2 escogiese la estrategia B, el jugador 1 escogería la estrategia A (como hemos visto antes) y el pago del jugador 2 será de 0.
El resultado del primer subjuego para el jugador 2 es de 5 si escoge la estrategia A y 0 si escoge la B. Tenemos pues, la solución al primer subjuego del jugador 2. Siempre escogerá la estrategia A frente a la B.
Faltaría ahora resolver la otra mitad del juego y habríamos resuelto todo.
Espero que con este ejemplo hayas entendido qué son los subjuegos y por qué son tan útiles para resolver problemas.
Jugador
Se considera jugador a cada uno de los individuos que participan en el juego y que tienen la capacidad de tomar decisiones dentro del mismo. No puede existir un juego sin jugadores, así que al menos deberá de haber uno para que algo pueda llamarse juego según la teoría de juegos.
Supuestos sobre los jugadores
Como hemos dicho antes, la teoría de juegos es una rama de las matemáticas aplicada a la realidad y, para poder hacer esto posible, tiene que partir de una serie de supuestos. Los supuestos son asunciones que se hacen para que el modelo pueda tener sentido matemáticamente hablando (es decir, que las ecuaciones no se contradigan).
Un supuesto fundamental sobre el que descansa la teoría de juegos es el de plena racionalidad de jugadores. Este supuesto quiere decir que, a la hora de plantear la resolución de cualquier juego, se tratará a cada jugador como si fuera un individuo perfectamente racional; que busca siempre escoger la mejor opción posible para sí mismo con la información de la que dispone en el momento de tomar la decisión.
Estrategia
Una estrategia es un plan de acción completo que seguirá un jugador a lo largo del juego. La principal característica de una estrategia es que contempla todas las opciones posibles que pueden tomar cada uno de los jugadores y, en base a esta información, ofrece el conjunto de jugadas que conducen al mejor resultado posible para un jugador en concreto.
Cuando se está resolviendo un juego, lo que se busca es descubrir las estrategias óptimas de cada jugador. Es decir, qué conjunto de jugadas hará cada jugador para obtener los mejores resultados posibles.
Hay que tener en cuenta que, como los jugadores son racionales, tendrán en cuenta las estrategias que escogerá su rival; por lo que es normal que muchos juegos se puedan resolver con una única estrategia óptima.
Pago
El pago es lo que cada jugador recibe como resultado del juego. Los pagos pueden ser positivos, representando ganancias, o negativos, representando pérdidas. Además, los pagos pueden ser conocidos o desconocidos por los jugadores a la hora de tomar sus decisiones. Un jugador puede verse en la obligación de escoger entre varias estrategias sin saber cual será el pago que él recibirá o sin saber cual será el pago que su rival recibirá.
Supuestos sobre los pagos
Al igual que en el caso de los jugadores, la teoría de juegos necesita otro supuesto sobre los pagos para poder tener sentido matemático. Este supuesto es el de cuantificación de los pagos. Es muy sencillo, para poder saber cuánto vamos a obtener por un juego, la unidad que se utilice para representar los pagos tiene que ser cuantificable.
Sé que parece obvio, sobre todo si piensas en pagos monetarios (el jugador A ganará 2€, el jugador B perderá 5€…), pero es un supuesto muy importante cuando los pagos no son dinero.
¿Qué es la cuantificación?
Imagina que el juego se plantea a la hora de escoger entre la carta de un restaurante. La satisfacción que obtendríamos por cada uno de los platos no puede expresarse como mucha, un poco y nada. No sería cuantificable. Es por esto que se debe de tomar una unidad, ficticia, para poder asignarle números y resolver el problema.
Recuerda, no podemos tener ecuaciones sin números, y la teoría de juegos es una rama de las matemáticas.

En este tipo de situaciones, se suele utilizar la unidad de medida ficticia favorita por los economistas, la “Utilidad”. Básicamente es una unidad inventada que representa, con números, la satisfacción que se obtiene de algo. Se mide en útiles y su escala es ficticia.
Así, los pagos del ejemplo anterior podrían ser de 100 útiles (mucha satisfacción), 20 útiles (poca satisfacción) y 0 útiles (nada de satisfacción). Pero también podría ser de 1.000, 200 y 0. Como ya hemos dicho, es una unidad ficticia; entonces no tiene una referencia real. Lo único que hay que entender es que funciona como una escala de puntuación, donde nosotros elegimos la escala. En el primer caso la escala iba del 100 al 0 y en el segundo del 1.000 al 0, pero significan lo mismo.
La utilidad también puede ser negativa (algunos economistas la llaman desutilidad), y simplemente representa las pérdidas de bienestar.
Información Disponible
Con información disponible nos referimos a la información a la que tienen acceso los jugadores a la hora de tomar sus decisiones.
Un jugador podría no saber cuales son los pagos asociados a cada una de las estrategias, por lo que en este caso, diríamos que la información es imperfecta. Este concepto es importante porque si un jugador no sabe el resultado del juego a la hora de tomar la decisión, su decisión variará.

Imagina que tenemos dos estrategias, la A y la B. Sabemos que en el juego se puede ganar dinero, pero también se puede perder. Si tomamos la estrategia A sabemos que nosotros ganaremos 100€ y nuestro rival ganará 500€. Si tomamos la B, sabemos que nuestro rival perderá 500€ (recibirá un pago de -500€) y nosotros no sabemos nuestro pago (recibiremos un pago de “?” ).
Según la teoría de juegos la opción óptima para nosotros sería la estrategia A, porque nos garantiza un pago seguro.
Ahora imagina que el pago “?” era de 1.000€, la opción óptima para nosotros seguiría siendo la que nos garantiza los 100€, porque a la hora de tomar la decisión no conocíamos el pago “?”; que perfectamente podría haber sido de -1.000€
Además de los pagos, los jugadores pueden desconocer el número de jugadores, las estrategias de las que disponen los jugadores o el número de veces que se repetirá el juego.
A los juegos en los que no disponemos de toda la información que existe se les conoce como juegos de información imperfecta (si hay datos que nadie conoce) o de información asimétrica (si un jugador tienen información que otro no tiene).
Información privilegiada
Este concepto simplemente muestra la información de la que disponen solo unos pocos jugadores con respecto al resto.
Es un concepto interesante desde la teoría de juegos, pues se pueden plantear juegos que determinen el precio máximo a pagar por la información privilegiada, de manera que tengamos un pago final mayor que si no pagásemos por la información privilegiada.
Equilibrio
Es el punto que se alcanza cuando los jugadores realizan sus jugadas (que, según el supuesto de individuos perfectamente racionales, serán las mejores posibles).

Existen muchos tipos de equilibrio, como el equilibrio perfecto o imperfecto y el equilibrio de Nash.
Este último es un equilibrio muy importante en la teoría de juegos, tanto que llevo John Nash a ganar el premio nobel. Hablaremos de este tipo de equilibrio, y del resto, en una sección especialmente dedicada a ellos.
Limitaciones de la Teoría de Juegos
Tipos de Juegos Según la Teoría de Juegos
Existen multitud de criterios para clasificar todos los posibles juegos que existen según la teoría de juegos. Estos son los criterios más comúnmente utilizados.
Sin embargo, recuerda que estos criterios no son excluyentes entre sí. Esto quiere decir que un juego, digamos cooperativo, también puede ser simultaneo y de una oportunidad.
De hecho, así es como se clasifican en la práctica, con multitud de etiquetas que definen con precisión que cabe esperar del juego en cuestión. Como ejemplo, clasifiquemos el clásico juego de piedra, papel o tijera. Este sería un juego no cooperativo, simultaneo y, si así deciden los jugadores, de una oportunidad.
Cooperativos o No cooperativos
Los juegos cooperativos son aquellos en los que los jugadores pueden interactuar entre sí, llegando a realizar coaliciones o grupos cooperativos antes de realizar sus respectivas jugadas. Algún ejemplo de este grupo tipo de juegos sería un interrogatorio policial, en el que los sujetos pueden hablar y ponerse de acuerdo antes de iniciar el juego.

En este tipo de juegos, la teoría de juegos se encarga de estudiar las interacciones entre grupos cuando los jugadores solo conocen las recompensas. La teoría se encarga de analizar las posibles estrategias de cooperación, comprendiendo cómo se forman los grupos y cómo se distribuirán las recompensas entre los grupos y entre los jugadores de cada grupo.
Por otro lado, los juegos no cooperativos son, como es evidente, lo opuesto. Se trata de juegos en los que los jugadores toman sus decisiones de manera aisladas, y en los que no está permitido formar grupos.
La teoría de juegos no cooperativos se centra en estudiar cómo los jugadores interactúan entre sí para alcanzar sus objetivos. El juego no cooperativo más común es el juego estratégico, donde solo se enumeran las estrategias disponibles y los resultados. Un ejemplo simplista es el piedra-papel-tijera.
Suma Cero
Los juegos de suma cero son aquellos en los que las ganancias totales que se pueden obtener en el juego por parte de un jugador son iguales a las pérdidas del resto de jugadores. La principal propiedad de este tipo de juegos es que se dedican a distribuir la riqueza, pero no a crearla.
Un ejemplo cotidiano de este tipo de juegos sería una timba de póker informal. En esta, todos los jugadores empiezan con el mismo dinero, y sus ganancias provienen de las pérdidas de otros jugadores. Otro ejemplo sería un juego en el que tiramos una moneda con un amigo y apostamos 1€. Nuevamente, la ganancia de un jugador será exactamente igual a las pérdidas de otro.
Los juegos de suma 0 se llaman así porque si sumamos el valor total de los pagos del juego, este será de 0; al no crearse ni perderse valor.

Muchas veces se considera a las inversiones en bolsa a corto plazo (inversiones que duran como mucho un par de semanas) como un juego de suma cero, ya que por la naturaleza de los contratos financieros, los incrementos de valor en un individuo necesariamente deben de ser pérdidas en otro. Sin embargo, a largo plazo la bolsa no puede considerarse como juego de suma cero, pues las empresas crecen y con ello incrementa su valor sin que nadie pierda dinero.
Por otro lado, los juegos de no suma cero son aquellos en los que todo el mundo puede ganar o perder. A diferencia de los juegos de suma 0, en los que por cada ganador hay un perdedor, en este tipo de juegos la cantidad de ganadores no influye en la de perdedores. El ejemplo más típico son los negocios.
Simultáneos o Secuenciales
Los juegos simultáneos son aquellos en los que los jugadores deben de hacer sus jugadas a la vez. Los secuenciales son, como es evidente, aquellos en los que los jugadores se turnan para realizar sus posibles jugadas.
Un ejemplo de juego simultáneo sería piedra, papel y tijera; pues los jugadores realizan su movimiento a la vez. Un ejemplo de juego secuencial podría ser el ajedrez o las damas; incluso el videojuego de Pokémon.

Una oportunidad o Repetitivos
Básicamente este criterio se refiere a la cantidad de veces que se puede repetir el juego en cuestión. Supongamos que un amigo apuesta con nosotros un euro a un juego de cara o cruz. Si al proponernos el juego, nos advierte de que solo podemos jugar una vez, estamos ante un juego con una única oportunidad. Sin embargo, si nuestro amigo nos ofrece jugar con él todas las veces que queramos, estaríamos ante un juego repetitivo.
Los juegos más importantes en la teoría de juegos
El Dilema del Prisionero
El Dilema del Prisionero es, probablemente, el ejemplo más conocido de la teoría de juegos.
Considera el caso de dos criminales arrestados por un delito. Los fiscales no tienen pruebas contundentes para condenarlos, pero se les ocurre una idea. Para obtener una confesión, los funcionarios sacan a los prisioneros de sus celdas solitarias e interrogan a cada uno en cámaras separadas. Ningún prisionero tiene la posibilidad de comunicarse con el otro. Los funcionarios les dan 4 alternativas.
A continuación tienes el juego representado de forma matricial:

Si ambos confiesan, recibirán una sentencia de prisión de ocho años cada uno. Si el Prisionero 1 confiesa, pero el Prisionero 2 no, el Prisionero 1 quedará libre y el Prisionero 2 recibirá diez años de cárcel. Lo mismo aplica para el Prisionero 2. Si ninguno confiesa, cada uno cumplirá un año en prisión.
La estrategia más favorable para ambos es no confesar. Sin embargo, ninguno está al tanto de la estrategia del otro y, sin certeza de que uno no confesará, es probable que ambos confiesen y reciban una sentencia de ocho años de prisión. El equilibrio de Nash (más adelante lo estudiaremos en detalle) de este juego sugiere que, si los dos prisioneros buscan su interés particular, ambos irán a la cárcel 8 años.
Nada impide a los prisioneros elegir mentir para evitarse muchos años de cárcel, pero hacerlo implica asumir el riesgo de ir diez años a la cárcel si la otra parte no elige hacer lo mismo.
El Juego del Dictador
El dilema del voluntario
El dilema del voluntario es un tipo de juego en el que alguien debe encargarse de una tarea o trabajo en pro del bien común. Además, para que un juego pueda considerarse que plantea un dilema del voluntario, el peor resultado posible se debe de obtener cuando nadie se ofrece como voluntario.

Un ejemplo podría ser un juego en el que todos los jugadores pueden elegir entre ganar 1€ o ganar 5€, pero en el que si ninguno elije ganar 1€ todos cobrarán 0€. El jugador que elija obtener 1€ en lugar de obtener 5€ sería el que se sacrifica por el grupo, pues perdería 4€ con respecto a sus compañeros.
Tomando ahora un ejemplo más propio del mundo real. Consideremos una empresa en la que el fraude contable es rampante, aunque la alta dirección no está al tanto. Algunos empleados del departamento de contabilidad son conscientes del fraude, pero dudan en informar a la alta dirección porque los empleados involucrados en el fraude serían despedidos.
Ser etiquetado como un “soplón” puede tener algunas repercusiones negativas a largo plazo. Pero si nadie se ofrece como voluntario, el fraude a gran escala puede resultar en la quiebra de la empresa y la pérdida de empleo de todos sus trabajadores.
El Juego del Ciempiés
El juego del ciempiés es un juego que toma lugar entre dos jugadores, A y B y que sirve para ejemplificar cómo existen juegos de información perfecta que solo pueden representarse de forma extensiva y nunca en forma matricial.
En el juego hay 2 montones de monedas, el primer montón tiene dos monedas y el segundo no tiene ninguna. Por turnos, cada jugador debe de elegir si quedarse con el montón más grande y dar el pequeño al contrario o si pasarle ambos. Cada vez que se escoge esta última opción, los montones crecen una moneda.
En el caso de escoger la primera opción, el juego termina y cada uno se queda con lo que haya en su montón. Si el juego llega al turno 100 sin que ninguno haya escogido la primera opción, el juego termina y ninguno gana nada. Por último, ambos jugadores saben lo que ocurrirá en el turno 100.
Se le conoce como juego del ciempiés porque no puede representarse en forma matricial, y al representarse en forma extensiva queda de la siguiente manera:
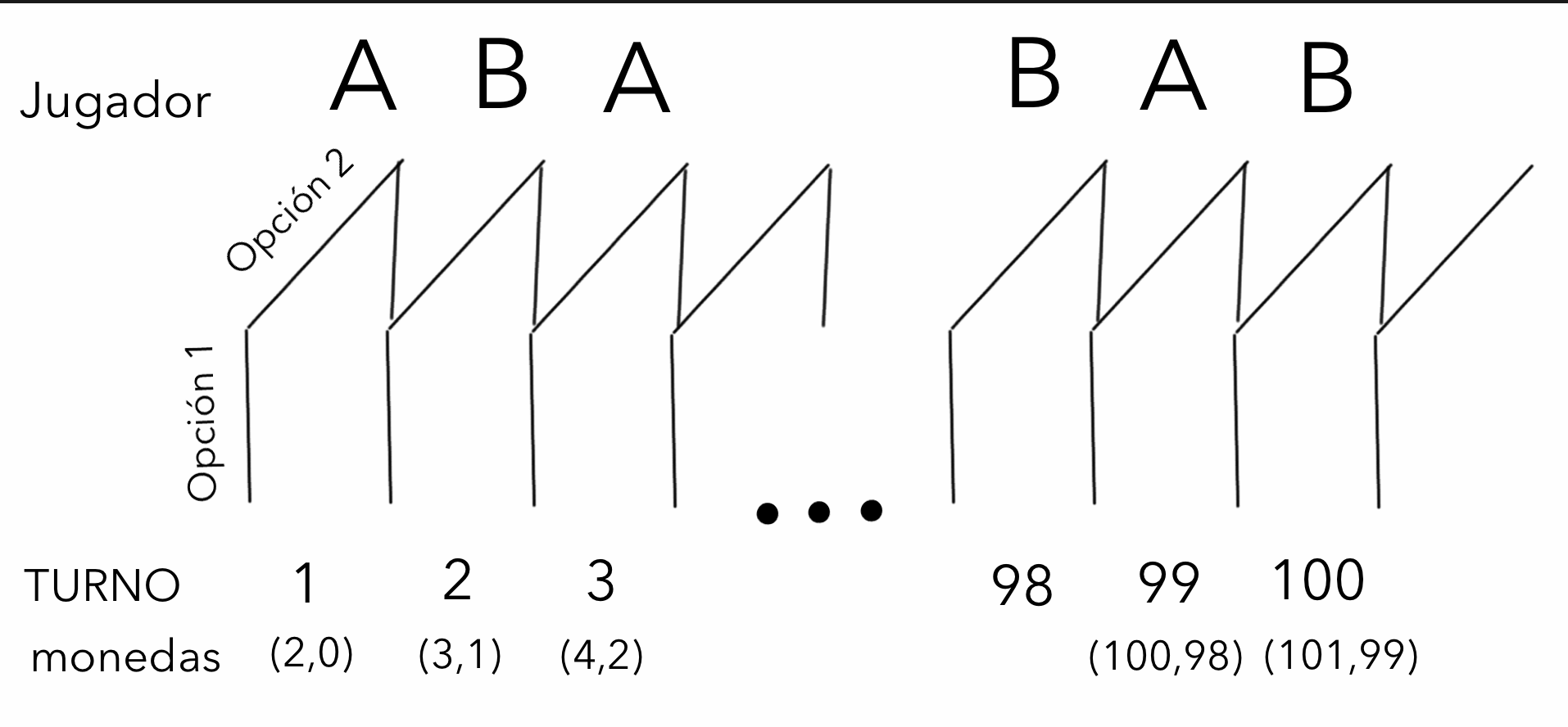
La relevancia de este juego para la teoría de juegos es que se observa una divergencia entre los resultados teóricos y empíricos, es decir, que la teoría dice que debería pasar una cosa pero en la práctica sucede otra distinta.
Tomando, una vez más, la premisa de plena racionalidad de los sujetos; el equilibrio de Nash de este juego (el punto al que conducen las mejores jugadas posibles) está en el primer turno, donde el jugador 1 acepta las dos monedas y finaliza el juego.
Tiene sentido si tenemos en cuenta que, jugadores plenamente “racionales” al buscar maximizar sus ingresos no correrán el riesgo de perder monedas por la osadía de su rival.
La teoría contra la práctica
El asunto de la racionalidad perfecta también es tópico presente en el debate académico, pues contradice algunos argumentos lógicos que demuestran la imposibilidad de que un sujeto sea íntegramente consistente con la “racionalidad”.
Evidentemente y en la práctica, nadie en su sano juicio perdería la oportunidad de ganar 100€ por una triste ganancia de 2€.
Es por esto que, en los laboratorios, se observaba como los jugadores prolongaban el juego hasta el turno 100, finalizando el mismo con unas ganancias de 101€ y 99€. Simplemente jugaban la opción 2 todo el rato hasta que llegase el turno 100 y jugaban la 1.
Los académicos han buscado explicaciones plausibles a esta divergencia tan absoluta entre la teoría y la práctica, sin poder encontrar una explicación satisfactoria.
Las principales aportaciones académicas debaten el echo de cómo está planteado el problema; discutiendo si el resultado diverge por la forma de plantear el problema o por no definir bien lo que se quiere estudiar en el mismo.
Opinión personal
Personalmente, opino que las divergencias entre la teoría y la práctica vienen dadas por la elevada rigidez y simplismo de la teoría. Es evidente que la cooperación nos garantiza unas ganancias de 100€, mientras que la competición nos garantiza unas de 2€; y esto es algo que la teoría de juegos no puede tener en cuenta.
No se puede esperar que todas las decisiones que se pueden tomar en un mundo tan complejo como el que vivimos se puedan reducir a una regla tan extremadamente simple como elegir la estrategia dominante; lo que nos impide ver el marco completo del problema.
Además, la teoría de juegos no plantea un enfoque de maximización de ganancias teniendo en cuenta la cooperación espontánea entre dos jugadores.
Este experimento es, quizás, uno de los más relevantes para la teoría de juegos; pues permite definir con mucha claridad dónde están los limites de la teoría y cómo debe de mejorarse.
Posibles Estrategias de Resolución de Problemas Según la Teoría de Juegos
Estrategia MaxiMax
Una estrategia maximax implica no aceptar resultados mediocres. Con esta estrategia, el jugador busca estar o totalmente dentro o totalmente fuera; o bien ganará mucho o enfrentará la peor consecuencia.
Veámoslo con un ejemplo. Consideremos una empresa que introduce un nuevo productos al mercado. El lanzamiento del producto puede mejorar la rentabilidad de la empresa en un 500% o llevarla a la ruina, ya que se ha invertido todo en este producto.
La elección de esta estrategia implicaría que el jugador este dispuesto a correr el riesgo de lograr el mejor resultado incluso si es posible el peor resultado.
Y aunque pueda parecer que esto no ocurre en la vida real, la creación de la famosa y lucrativa marca “Jordan” siguió esta estrategia.
Estrategia Maximin
Una estrategia Maximin en teoría de juegos resulta en que el participante elija el mejor de los peores resultados. Se traduce a una estrategia de minimización de pérdidas.
Es la estrategia opuesta a la anterior. En esta, el jugador busca disminuir la incertidumbre, sacrificando el potencial beneficio a cambio.
A menudo, las empresas enfrentan y aceptan esta estrategia al considerar demandas legales. Al llegar a un acuerdo fuera de los tribunales y evitar un juicio público, las empresas aceptan un resultado desfavorable. Sin embargo, ese resultado podría haber sido peor si el caso hubiera llegado a juicio.
Estrategia Dominante
Una estrategia dominante es aquella que garantiza el mejor resultado posible al jugador, independientemente de la jugada de su rival.
Por ejemplo, en un juego el jugador 1 puede escoger la estrategia A, con la que ganará 1€ si el jugador 2 juega también la A o 2€ si juega la B. Por otro lado, el jugador 1 también puede escoger la estrategia B, con la que ganará 5€ y el jugador 2 juega la A o 10€ si juega la B. En este caso, para el jugador 1 la estrategia B domina a la A y siempre deberá escogerla según la teoría de juegos.
Estrategia Pura
Una estrategia pura se puede traducir como la existencia de una decisión específica y concreta en la estrategia de un jugador. Es decir, es una estrategia en la que no interviene nunca el azar.
Por ejemplo, en un juego de piedra, papel o tijeras, elegir tijeras como tu movimiento sería una estrategia pura. En un juego de cara o cruz que se jugará 3 veces, escoger cara, cruz y cruz como respuesta también sería una estrategia pura.
Estrategia Mixta
Equilibrio de Nash
¿Qué es el equilibrio de Nash?
El concepto de equilibrio de Nash le supuso ganar el premio nobel al matemático John Nash.
Sin entrar en complicaciones sobre los modelos matemáticos que utilizó, podemos definir el equilibrio de Nash como una situación en la que todos los jugadores (conscientes de haberlo hecho) han escogido las mejores jugadas posibles a nivel individual. De este modo, ningún jugador tiene incentivos para variar sus jugadas.
Es muy importante tener en cuenta que, pese a haberse alcanzado un equilibrio de Nash, esto no implica que los jugadores obtengan el mejor resultado posible.
Sí, sé que suena un poco contradictorio; pero permíteme explicarlo. El equilibrio de Nash se alcanza cuando los jugadores persiguen el mejor resultado individualmente; sin plantearse situaciones alternativas en las que si ambos cooperan podrían maximizar sus ganancias.
Es perfectamente posible (como veremos en el siguiente ejemplo) que el equilibrio de Nash no garantice el mejor resultado posible y, sin embargo, los jugadores sigan sin variar sus jugadas.
Ejemplos de Equilibrio de Nash
Como no, como ejemplo para explicar el equilibrio de Nash tomaremos nuevamente el dilema del prisionero.
Ya sabemos en qué consiste, pero lo resumiré muy rápidamente por si alguien se ha perdido por el camino.
Tenemos 2 presos, que pueden elegir entre mentir por sus crímenes o confesar y delatar con ello a su compañero. No hay pruebas sólidas contra ellos, por lo que solo irán a la cárcel durante un si ninguno confiesan.
En caso de que confiesen, el “soplón” quedará libre y su compañero será encarcelado durante 10 años. Si ambos confiesan (lo que interesa a los policías que han ideado este juego) ambos irán a la cárcel durante 8 años. Está, incomunicados cuando se les explica esta situación.
Aquí tienes el juego representado en forma matricial:

El equilibrio de Nash
Bien, teniendo en cuenta el supuesto de racionalidad de los jugadores, sabemos que buscarán minimizar sus años de encarcelamiento a toda costa.
Podemos ver que, para ambos jugadores, la estrategia de confesar reporta o 8 años de cárcel o ninguno. Mientras que la de mentir reporta o 10 años de cárcel o 1.
La estrategia de confesar domina a la de mentir, por lo que ambos deberían de elegir confesar. De este modo se alcanza un equilibrio de Nash, pues los dos jugadores han realizado las jugadas que individualmente les garantizan los mejores resultados.
En el equilibrio de Nash los dos jugadores irán a la cárcel durante 8 años y la policía habrá ganado con su perspicaz idea.
El mejor resultado posible
Si nos fijamos bien, existe una posibilidad de que los dos prisioneros tengan un mejor destino. Podrían ir a la cárcel solo durante un año, y no tendrían que tener el cargo de conciencia de haber delatado a su amigo.
Para que este resultado sea posible tendrían que ocurrir alguna de estas dos cosas:
- Que los jugadores, de algún modo, se hubiesen podido comunicar antes de tomar su decisión. De este modo podrían haber ideado una estrategia conjunta y evitado caer en la trampa de la policía.
- Que los dos jugadores no se ajusten al supuesto de “plena racionalidad” en el sentido estricto (aunque nuevamente podríamos entrar en debate sobre si ir a la cárcel 8 años es más racional que hacerlo durante 1). Si esto ocurriese, valores como el compañerismo, o el miedo a las consecuencias de ser un “soplón” podrían invitar a los sujetos a mentir y alcanzar el mejor resultado posible
Ahora ya entiendes qué es el equilibrio de Nash y porque no necesariamente implica la mejor estrategia posible.
Tipos de Equilibrio de Nash
Equilibrio de Nash Perfecto en Subjuegos
Ahora que entendemos con claridad lo que es un equilibrio de Nash, es muy sencillo comprender qué es un equilibrio de Nash perfecto en subjuegos.
Es simplemente un equilibrio de Nash que tiene lugar en un subjuego.
Cuando hemos hablado del concepto de subjuego y lo hemos utilizado para resolver un problema de teoría de juegos, lo que estábamos haciendo para “resolver” estos subjuegos era simplemente encontrar su equilibrio de Nash.
Como has podido ver, es muy útil; pues gracias a estos equilibrios de Nash perfectos en subjuegos hemos podido simplificar el juego poco a poco hasta llegar al equilibrio de Nash.
Equilibrio de Nash en Estrategias Puras
Aplicando la misma lógica anterior, y todo lo que ya sabemos sobre teoría de juegos, podemos deducir que un equilibrio de Nash en estrategias puras es simplemente un equilibrio de Nash que se alcanza siguiendo una estrategia pura.
Básicamente podremos decir que nos encontramos ante un equilibrio de Nash en estrategias puras cuando, para formular “solución del juego” (el equilibrio de Nash); lo hagamos sin necesidad de incluir probabilidades.
Equilibrio de Nash en Estrategias Mixtas
Del mismo modo que antes, el equilibrio de Nash en estrategias mixtas tendrá lugar cuando; para formular el equilibrio de Nash de un juego, tengamos que recurrir al uso de probabilidades.
Por ejemplo, si para formular el equilibrio de Nash de un juego necesitamos decir: “El jugador 1 jugará la estrategia A el 80% de las veces y la estrategia B el 20% restante”, entonces nos encontramos ante un equilibrio de Nash en estrategas mixtas.
Aplicaciones de la Teoría de Juegos
Economía
La teoría de juegos supuso una revolución en la disciplina económica, pues permitía analizar problemas en los modelos matemáticos aplicados a la economía previos a esta teoría. Por ejemplo, la escuela económica neoclásica [link], que resumida muy brevemente es una rama que cuenta con los modelos matemáticos más precisos, pero también más irreales; no podía analizar la competencia imperfecta. La teoría de juegos permitió cambiar el foco de atención del equilibrio de los mercados al proceso de toma de decisiones en los mercados.
Negocios
En la rama de los negocios, la teoría de juegos sirve para modelar los comportamientos competitivos entre agentes económicos.
Normalmente, las empresas deben elegir entre varias opciones estratégicas que afectarán a sus beneficios. Por ejemplo, las empresas pueden enfrentarse a dilemas como retirar productos existentes y desarrollar nuevos o emplear nuevas estrategias de marketing.
Las empresas también pueden elegir sus competidores a la hora de entrar en un mercado. Las empresas siempre están compitiendo por recursos, intentando contratar a los mejores candidatos de sus rivales y captar la atención de los clientes lejos de productos competidores; y la teoría de juegos es perfecta para estas decisiones.
La teoría de juegos en los negocios suele parecerse más a un árbol de juegos, como se muestra a continuación. Una empresa puede comenzar en la posición uno y debe decidir entre dos resultados. Sin embargo, siempre hay otros factores que se deben de tener en cuenta.
Gestión de proyectos
La gestión de proyectos se sirve de la teoría de juegos en la medida en la que las decisiones de cada uno de los participantes en el proyecto influyen en el resultado final. Esto es importante porque cada miembro del proyecto podría tener intereses distintos que condicionen su desarrollo.
Por ejemplo, un gestor de un proyecto de obra podría estar incentivado a completar el proyecto de una manera rápida y eficaz. Mientras que el trabajador podría estarlo nen trabajar lentamente por su seguridad o para retrasar el fin del proyecto y acumular más horas de trabajo.
En el caso de un equipo interno, la teoría se vuelve menos relevante, pues por lo general los participantes del grupo suelen tener intereses comunes. Sin embargo, los consultores externos o grupos de colaboración ajenos a la empresa podrían tener unos intereses muy distintos a los del grupo.
Estrategias de fijación de precios
El mejor ejemplo posible podría ser el Black Friday. El concepto en el que se fundamenta es de que la reducción de precios implica una mayor cantidad de consumidores comprando una mayor cantidad de bienes.
La relación entre consumidor, bienes y el intercambio financiero juega un papel fundamental en la teoría de juegos, pues cada consumidor tiene diferentes expectativas y toma decisiones en función de diversas variables.
A parte de para fijar el precio en las campañas promocionales, la teoría de juegos es especialmente útil cuando se prevé una guerra de precios con una compañía rival. Fijar un precio muy bajo podría suponer no tener ningún beneficio, pero poner uno demasiado alto podría suponer que los consumidores eligiesen a la competencia.
Si has llegado hasta aquí, me gustaría darte las gracias personalmente. Espero que este artículo te haya gustado y espero que hayas aprendido un montón sobre la teoría de juegos.
Si sigues con ganas de aprender, estoy seguro de que este artículo sobre Precios Ancla y Marketing te va a encantar. Y tranquilo, este artículo es mucho más corto.
Este artículo ha sido escrito por Darío Talaya Ballesteros, licenciado en ciencias económicas y empresariales y en el Master Universitario en Estrategia y Marketing de la Empresa (MUEME) por la Universidad de Castilla-La Mancha (UCLM).
En colaboración con la consultoría de marketing digital Cuartero Agurcia y, en especial, con Lissbeth Reyes Agurcia y Alberto Martínez Cuartero.